
|
公共教育学院(马克思主义学院)
|
随机事件与概率
1.事件的关系 ![]()
2.运算规则 (1)![]()
(2)![]()
(3)![]()
(4)![]()
3.概率![]() 满足的三条公理及性质:
满足的三条公理及性质:
(1)![]() (2)
(2)![]()
(3)对互不相容的事件![]() ,有
,有![]() (
(![]() 可以取
可以取![]() )
)
(4)![]() (5)
(5)![]()
(6)![]() ,若
,若![]() ,则
,则![]() ,
,![]()
(7)![]()
(8)![]()
4.古典概型:基本事件有限且等可能
5.几何概率
6.条件概率
定义:若![]() ,则
,则![]()
乘法公式:![]()
若![]() 为完备事件组,
为完备事件组,![]() ,则有
,则有
全概率公式: ![]()
Bayes公式:![]()
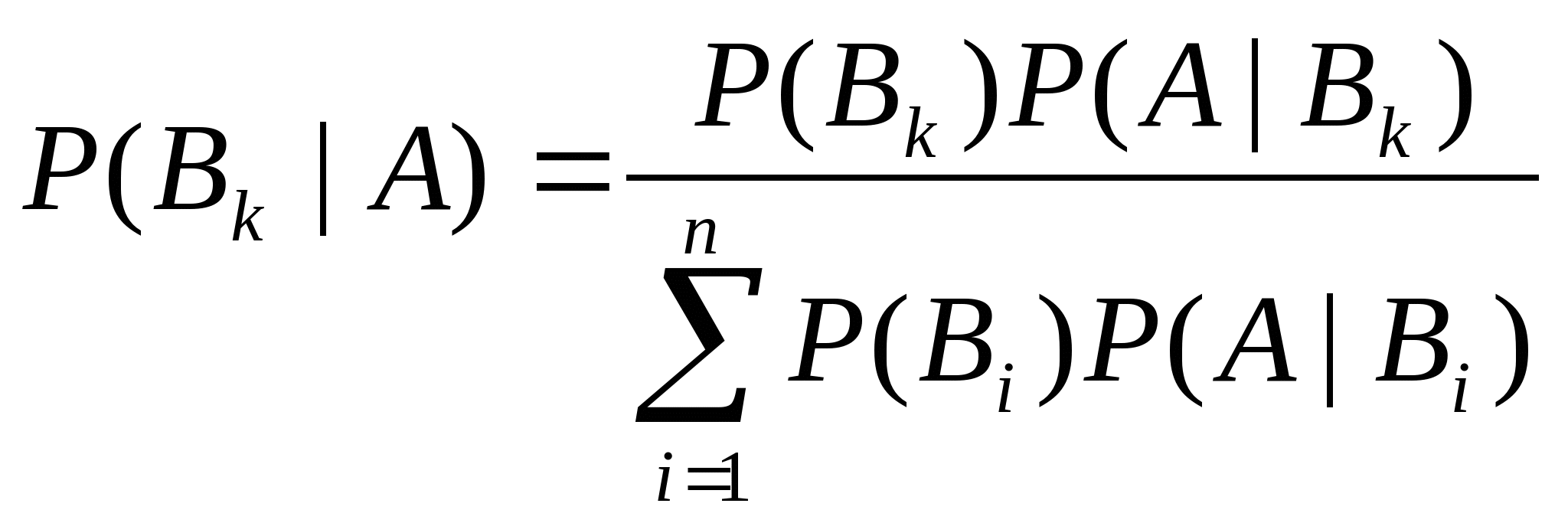
7.事件的独立性: ![]() 独立
独立![]() (注意独立性的应用)
(注意独立性的应用)
第二章 随机变量与概率分布
离散随机变量:取有限或可列个值,![]() 满足(1)
满足(1)![]() ,(2)
,(2)![]() =1
=1
(3)对任意![]() ,
,![]()
连续随机变量:具有概率密度函数![]() ,满足(1)
,满足(1)![]() ;
;
(2)![]() ;(3)对任意
;(3)对任意![]() ,
,![]()
几个常用随机变量
名称与记号 | 分布列或密度 | 数学期望 | 方差 |
两点分布 |
|
|
|
二项式分布 |
|
|
|
Poisson分布 |
|
|
|
几何分布 |
|
|
|
均匀分布 |
|
|
|
指数分布 |
|
|
|
正态分布 |
|
|
|
分布函数 ![]() ,具有以下性质
,具有以下性质
(1)![]() ;(2)单调非降;(3)右连续;
;(2)单调非降;(3)右连续;
(4)![]() ,特别
,特别![]() ;
;
(5)对离散随机变量,![]() ;
;
(6)对连续随机变量,![]() 为连续函数,且在
为连续函数,且在![]() 连续点上,
连续点上,![]()
正态分布的概率计算 以![]() 记标准正态分布
记标准正态分布![]() 的分布函数,则有
的分布函数,则有
(1)![]() ;(2)
;(2)![]() ;(3)若
;(3)若![]() ,则
,则![]() ;
;
(4)以![]() 记标准正态分布
记标准正态分布![]() 的上侧
的上侧![]() 分位数,则
分位数,则![]()
随机变量的函数 ![]()
(1)离散时,求![]() 的值,将相同的概率相加;
的值,将相同的概率相加;
(2)![]() 连续,
连续,![]() 在
在![]() 的取值范围内严格单调,且有一阶连续导数,则
的取值范围内严格单调,且有一阶连续导数,则![]() ,若不单调,先求分布函数,再求导。
,若不单调,先求分布函数,再求导。
第三章 随机向量
二维离散随机向量,联合分布列![]() ,边缘分布列
,边缘分布列![]() ,
,![]() 有
有
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]()
二维连续随机向量,联合密度![]() ,边缘密度
,边缘密度![]() ,有
,有
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() ,
,![]()
二维均匀分布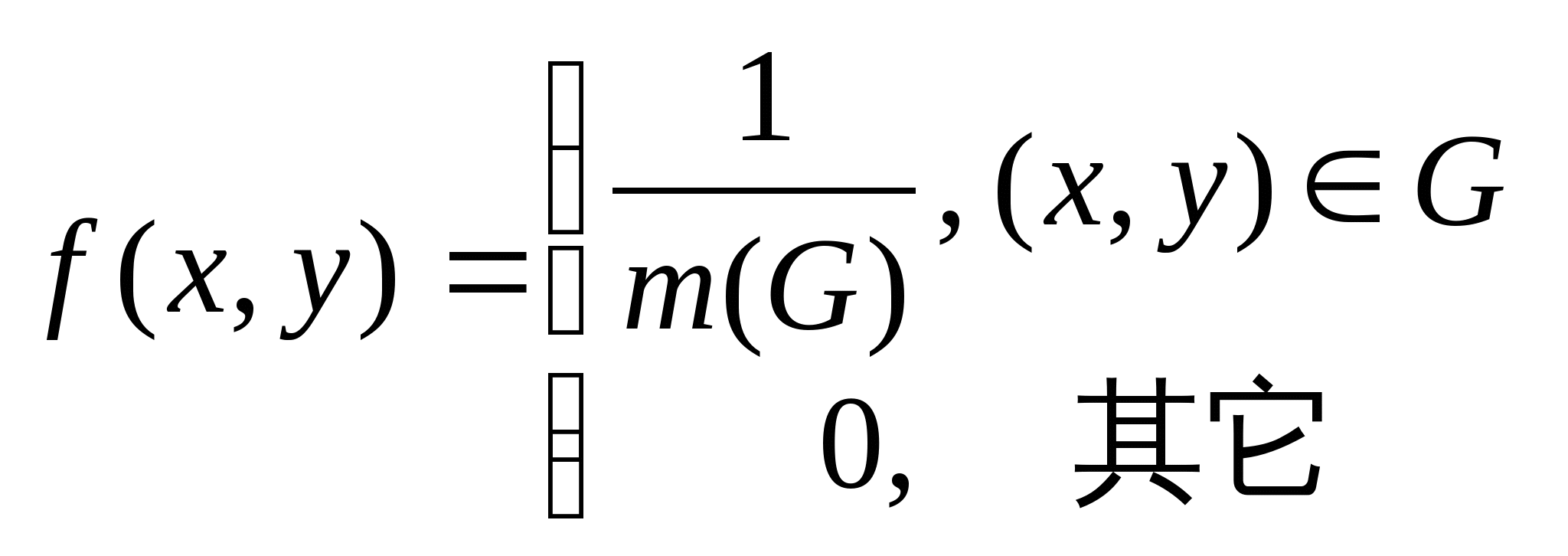 ,其中
,其中![]() 为
为![]() 的面积
的面积
二维正态分布![]() ,其密度函数(牢记五个参数的含义)
,其密度函数(牢记五个参数的含义)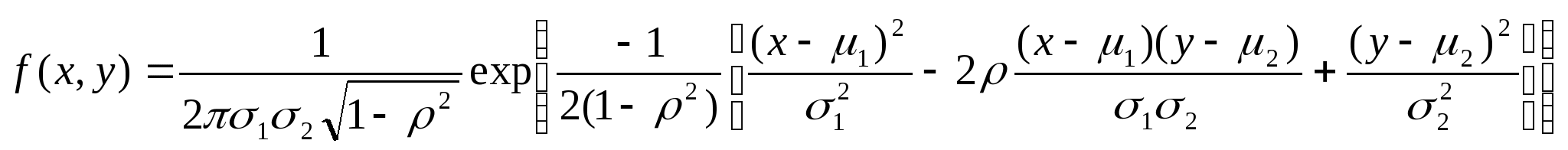 且
且![]() ;
;
二维随机向量的分布函数 ![]() 有
有
(1)关于![]() 单调非降;(2)关于
单调非降;(2)关于![]() 右连续;
右连续;
(3)![]() ;
;
(4)![]() ,
,![]() ,
,![]() ;
;
(5)![]() ;
;
(6)对二维连续随机向量,![]()
6.随机变量的独立性 ![]() 独立
独立![]()
离散时 ![]() 独立
独立![]()
连续时 ![]() 独立
独立![]()
二维正态分布![]() 独立
独立![]() ,且
,且![]()
7.随机变量的函数分布
和的分布 ![]() 的密度
的密度![]()
最大最小分布
第四章 随机变量的数字特征
1.期望
(1)离散时 ![]() ,
,![]() ;
;
(2)连续时![]() ,
,![]() ;
;
(3)二维时![]() ,
,![]()
(4)![]() ;(5)
;(5)![]() ;
;
(6)![]() ;
;
(7)![]() 独立时,
独立时,![]()
2.方差
(1)方差![]() ,标准差
,标准差![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() 独立时,
独立时,![]()
3.协方差
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() 时,称
时,称![]() 不相关,独立
不相关,独立![]() 不相关,反之不成立,但正态时等价;
不相关,反之不成立,但正态时等价;
(5)![]()
4.相关系数 ![]() ;有
;有![]() ,
,![]()
5.![]() 阶原点矩
阶原点矩![]() ,
,![]() 阶中心矩
阶中心矩![]()
第五章 大数定律与中心极限定理
1.Chebyshev不等式 ![]() 或
或![]()
2.大数定律
3.中心极限定理
(1)设随机变量![]() 独立同分布
独立同分布![]() ,则
,则![]() , 或
, 或![]() 或
或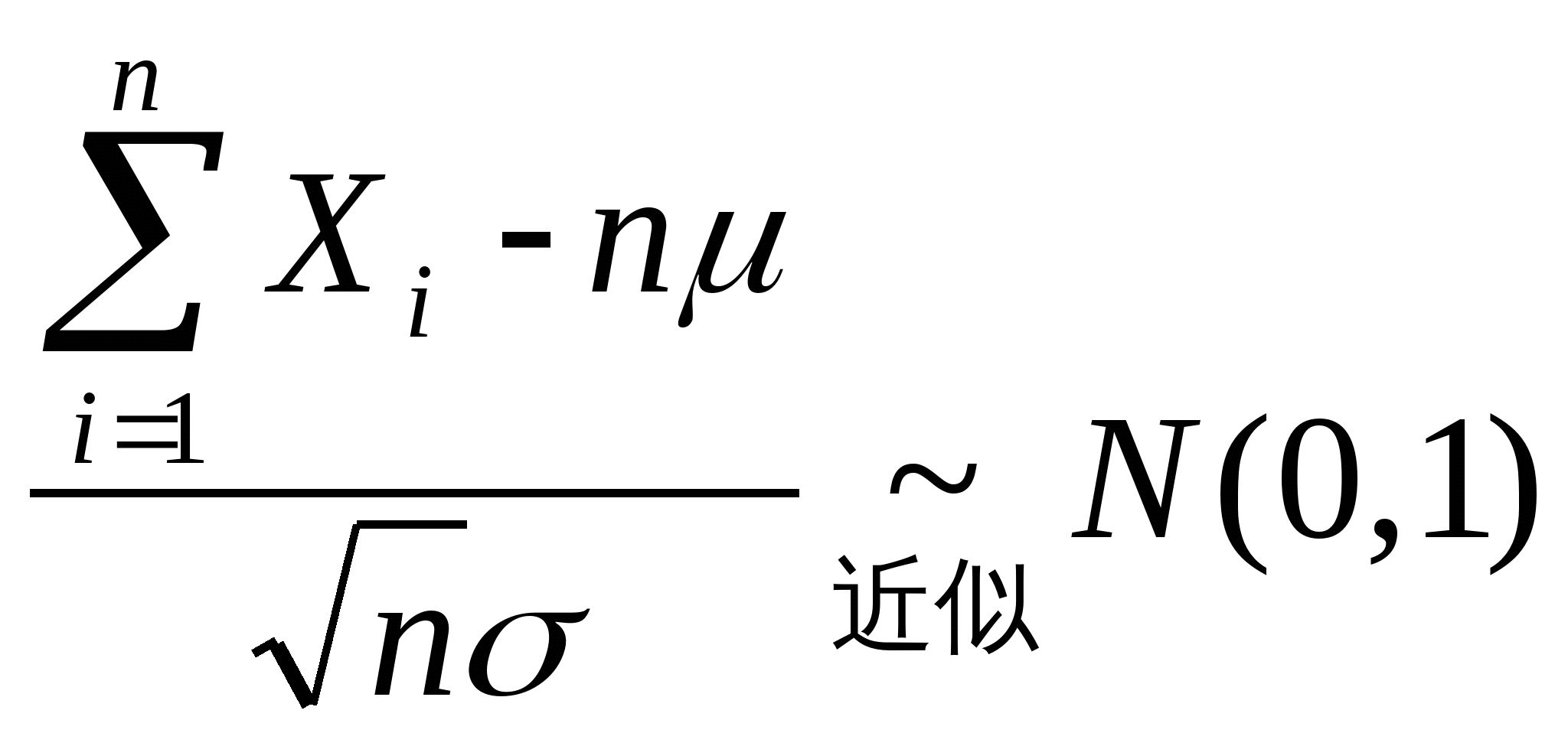 ,
,
(2)设![]() 是
是![]() 次独立重复试验中
次独立重复试验中![]() 发生的次数,
发生的次数,![]() ,则对任意
,则对任意![]() ,有
,有![]() 或理解为若
或理解为若![]() ,则
,则![]()
第六章 样本及抽样分布
1.总体、样本
简单随机样本:即独立同分布于总体的分布(注意样本分布的求法);
样本数字特征:
样本均值![]()
![]() (
(![]() ,
,![]() );
);
样本方差![]() (
(![]() )样本标准差
)样本标准差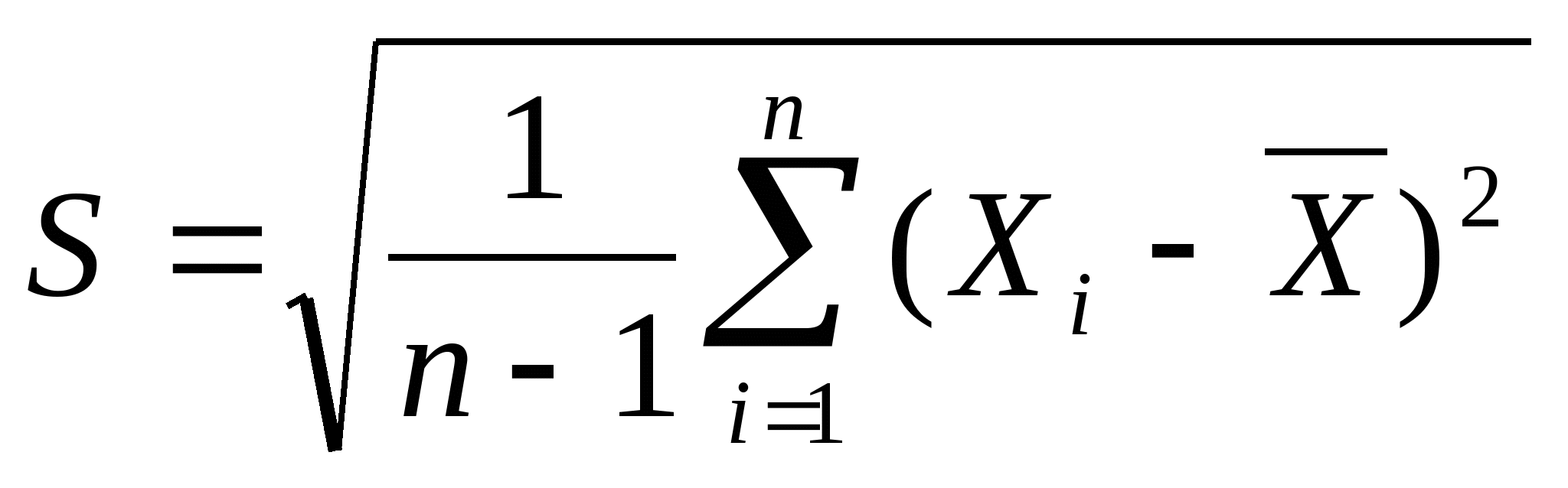
样本![]() 阶原点矩
阶原点矩![]() ,样本
,样本![]() 阶中心矩
阶中心矩![]()
2.统计量:样本的函数且不包含任何未知数
3.三个常用分布(注意它们的密度函数形状及分位点定义)
(1)![]() 分布
分布 ![]() ,其中
,其中![]() 独立同分布于标准正态分布
独立同分布于标准正态分布![]() ,若
,若![]() 且独立,则
且独立,则![]() ;
;
(2)![]() 分布
分布 ![]() ,其中
,其中![]() 且独立;
且独立;
(3)![]() 分布
分布 ![]() ,其中
,其中![]() 且独立,有下面的性质
且独立,有下面的性质 ![]()
4.正态总体的抽样分布
(1)![]() ; (2)
; (2)![]() ;
;
(3)![]() 且与
且与![]() 独立;
独立; ![]() (4)
(4)![]() ;
;
(5)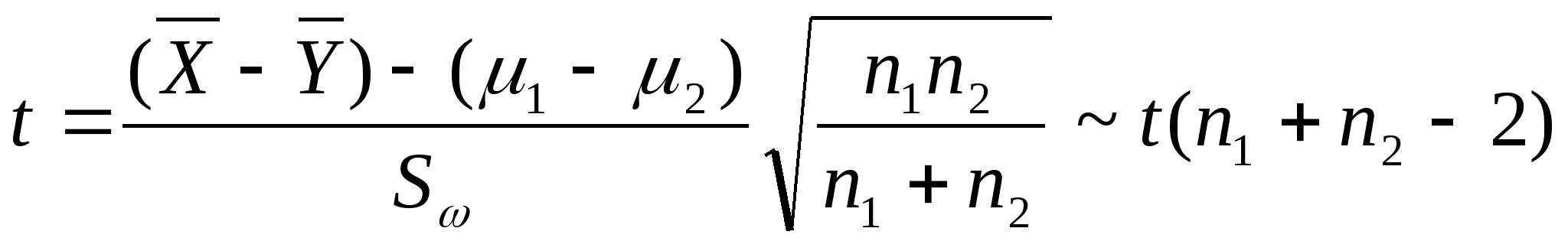 ,
,![]()
(6)![]()
第七章 参数估计
1.矩估计:
(1)根据参数个数求总体的矩;(2)令总体的矩等于样本的矩;(3)解方程求出矩估计
2.极大似然估计:
(1)写出极大似然函数;(2)求对数极大似然函数(3)求导数或偏导数;(4)令导数或偏导数为0,解出极大似然估计(如无解回到(1)直接求最大值,一般为min![]() 或max
或max![]() )
)
3.估计量的评选原则
(1)无偏性:若![]() ,则为无偏; (2)有效性:两个无偏估计中方差小的有效;
,则为无偏; (2)有效性:两个无偏估计中方差小的有效;
4.参数的区间估计(正态)
参数 | 条件 | 估计函数 | 置信区间 |
|
|
|
|
|
|
| |
|
|
|
|